Joy's Personal Website

Verifiable Delay Function Explained with Applications

Wed Jan 17, 2024
crypto

Verifiable Delay Function Explained with Applications

Verifiable Delay Function is a useful cryptographic primitive that has a wide range of applications such as randomness beacon and proof of replication. Similar to zero knowledge proving systems, the output of a verifiable delay function is slow to compute and requires sequential computation, but can be efficiently verified. Unlike Proof of Work that parallel work can be performed across different machines, VDF is required to perform sequentially and cannot be parallelized.

We first define what is a verifiable delay function, then discuss its required properties. Then we go over a few constructions that are widely deployed in applications and a CLI tool for an example.

We start with a naive VDF construction chaining hash functions, i.e. output = H(H(H...H(A))). To compute the output, the evaluation cannot be parallelized, because the result of a previous step is used as an input for the current step. However, to verify the result it is required to compute the chaining again, so it is not efficient to verify.

Definitions and Properties

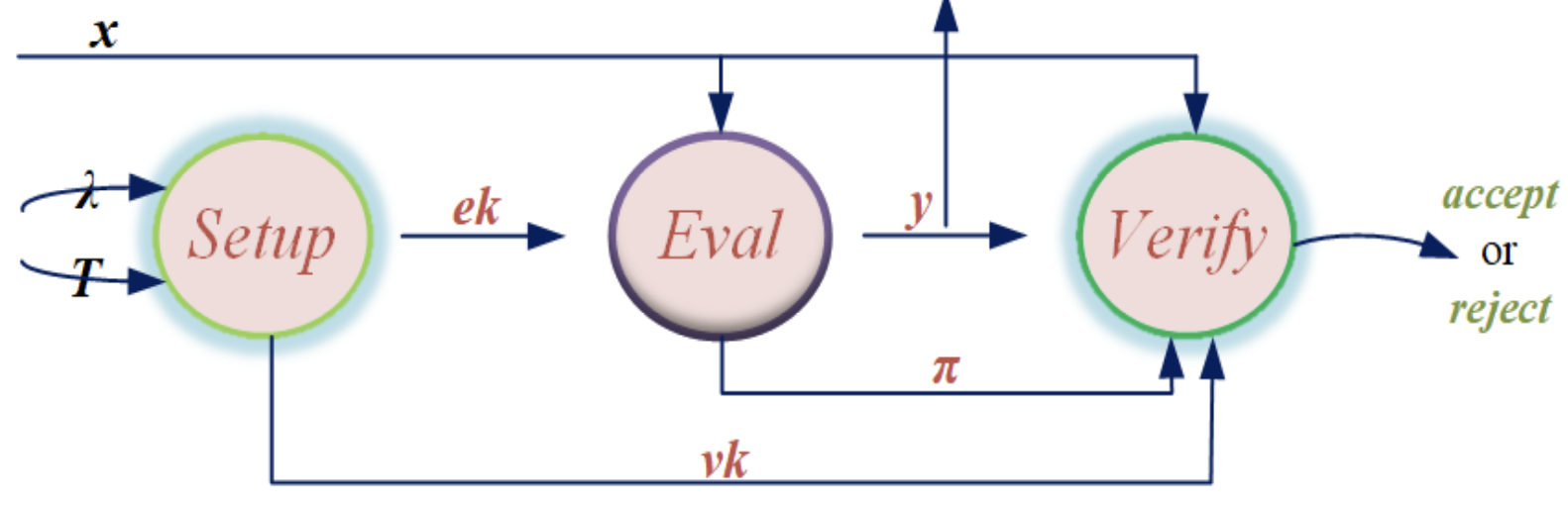
A VDF is defined as a tuple of the following 3 functions:

  1. setup(param) => (ek, vk): Given a parameter, outputs an evaluation key and a verifying key.

  2. eval(ek, x) => y, pi: Using an input and the evaluation key, evaluate to an output and a proof. Note this step is sequential and cannot be parallelized.

  3. verify(vk, x, y, pi) => true/false: Using the verifying key, input, output, and the proof, verifies that the output is indeed computed from the input.

Algorithms for VDF

What are the required properties for the VDF algorithms?

  1. Correctness: A correct output should always be verified.

  2. Soundness: The possibility to verify an incorrect output is negligible.

  3. Sequentiality: An honest party can evaluate the output in t sequential steps.

  4. Decodability: Given the output, proof and the evaluation key, the input can be decoded.

  5. Incremental: Using the same ek and vk, different difficulties can be supported. That is, the time parameter is only required at the evaluation step, not the setup, so a different time delay does not require a different setup.

Weak vs. Strong VDF

We distinguish weak and strong VDF here, this is useful for certain constructions discussed later. A weak VDF allows for a certain amount of parallelism is needed to give an advantage.

Popular Constructions

Wesolowski’s VDF

This construction can be first defined as an interactive protocol, then it can be transformed to a non-interactive one via Fiat Shamir Heuristics.

First we define $g$ is a group element in group G of an unknown finite order for which both input and output of VDF is in.

The evaluation step computes $y = g^{2^t}$. Then pick a random prime $l$ that is in ${1…2^{2\lambda}}$. Output $y$ and its evaluation proof $\pi = g^{2^t/l}$. Why is this slow to compute? Because $g$ has unknown order, that is, we do not know $|G|$ so fast exponentiation is not possible. Otherwise we can reduce it to $g^{2^t \mod |G|}$ then we have $2^{|G|} = 1$.

The verification step first computes: $r = 2^t \mod l$, then checks $\pi^l \cdot g^r = y$. This is relatively fast to run.

To choose the group G, there are generally two options.

  1. RSA: Use $N = p \cdot q$. This makes the evaluation step slow to compute since p and q are unknown. This requires an MPC trusted setup such that no party should learn the factorization p, q.

  2. Class groups of an imaginary quadratic field: This describes a group that are the quotients of $P(K)/I(K)$ where $K$ is a number field and $I(K)$ is the set of fractional ideals of K. We will leave out the algebraic details here, but we know this does not require a trusted setup and we need to define a large prime discriminant.

A Very Similar one: Pietrzak

To run setup, first we choose a time parameter $T$, a finite abelian group $G$ of unknown order and a hash bytes to element function H. (Same as Wesolowski’s.)

To evaluate the output, compute $y = g^(2^(T/2))$ where $g = H(x)$. This step takes $O(\sqrt{T})$ group operations, which is slightly more efficient than Wesolowski’s that takes $O(T)$.

To verify the output and proof, the verifier first picks $r$ in ${1, … 2^l}$, then check: $v^r * z = (g^r * v)^{2^{T/2}}$.

  1. Univariate permutation polynomials

This construction uses the conclusion that given a permutation polynomial of degree t over finite field $F_p$, inverting it requires computing a polynomial GCD which is time extensive and sequential. It takes $O(log(p))$ multiplications of dense polynomials and it cannot be done in t steps on at most $O(t^2)$ processors. This is considered a weak VDF since there can be some parallelization.

  1. Isogeny-based VDF

This class of construction requires more advanced cryptographic knowledge to understand. On a high level, the evaluation step is a random walk of length depending on difficulty. The verification step leverages pairings which can be done very quickly.

Applications

  1. Randomness beacon

Randomness beacon describes the last revealer advantage problem when generating randomness collectively. When each party is committed to the partial randomness, the last revealer can wait and decide whether to reveal his partial randomness based on the aggregated randomness result.

To make the randomness unbiased and hard to manipulate, we use an VDF phase immediately after all parties revealed their randomness. This is to prevent anyone from anticipating what the next seed might be, because the fast hash function is replaced by a very long computation.

One specific example is leader election during proof of stake consensus. The leader is selected based on the output of VDF after all validators contributed their randomness. Ethereum uses VDF for leader election with strong safety and liveness guarantee.

  1. Proof of data replication

Proof of replication is an application that requires the server to dedicate unique storage for the data even if the data is available from another public source.

Recall that for a decodable verifiable delay function, the evaluation should take a long time but the decoding is relatively fast.

When storing the data, the server first breaks the data into n blocks (b_1…b_n) and make n evaluations (y_1…y_n) where y_i = eval(ek, b_i || H(id || i)). When a verifier requests a copy, the server can return y_i and the verifier can quickly get the b_i with fast decoding. Note that if the server has not stored the data it cannot return y_i, even though it might get b_i from the public. Therefore this scheme ensures the unique storage of certain data.

Try it out

Here we use the CLI provided by this repo. This implements Wesolowskis’ VDF construction discussed before.

cargo build --bin vdf-cli

target/debug/vdf-cli evaluate --discriminant cd711f181153e08e08e5ba156db0c4e9469de76f2bd6b64f068f5007918727f5eaa5f6a0e090f82682a4ebf87befdea8f1253265d700ee3ca6b0fdb2677c633c7f37b62f0e0c13b402def0ba9abaf15e4c53bfb6bda0c7a0cad4439864af3eb9af6d6c4b10286eb8ff5e2de5b009196bc60c3000fde8d4b89b7674e61bc2d23f --iterations 10
Output: 0000c7494cc791f1c26547fd9deb5d6fa73bc30895bea883f4a6d411e3c5ad004c80abb8dc3ddc0dd5311b74f7ade87eb219a80c9157bb8969b140e7cd2ea9c4330647e4afcdeb5d1c90596c009a31e4d81a11245a1957b21ae46f9e2b4ddcd7e4081001
Proof:  04000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000


target/debug/vdf-cli verify --discriminant cd711f181153e08e08e5ba156db0c4e9469de76f2bd6b64f068f5007918727f5eaa5f6a0e090f82682a4ebf87befdea8f1253265d700ee3ca6b0fdb2677c633c7f37b62f0e0c13b402def0ba9abaf15e4c53bfb6bda0c7a0cad4439864af3eb9af6d6c4b10286eb8ff5e2de5b009196bc60c3000fde8d4b89b7674e61bc2d23f --iterations 10 --
output 0000c7494cc791f1c26547fd9deb5d6fa73bc30895bea883f4a6d411e3c5ad004c80abb8dc3ddc0dd5311b74f7ade87eb219a80c9157bb8969b140e7cd2ea9c4330647e4afcdeb5d1c90596c009a31e4d81a11245a1957b21ae46f9e2b4ddcd7e4081001 --proof 04000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Verified: true

References

  1. Paper: https://eprint.iacr.org/2018/601.pdf

  2. Walkthrough: https://medium.com/iovlabs-innovation-stories/verifiable-delay-functions-8eb6390c5f4

  3. Ethereum discussion: https://ethresear.ch/t/verifiable-delay-functions-and-attacks/2365/8

  4. Paper: https://www.mdpi.com/1424-8220/22/19/7524

  5. Survey of the first two VDF constructions: https://eprint.iacr.org/2018/712.pdf