An overview of Secure Multi-Party Computation use cases in cryptocurrency.

Multi-Party Computation describes the techniques that a number of parties with private inputs wish to compute a joint function of their inputs, without revealing anything but the output. A simple example is A and B would like to find who has more money in the bank account without needing to tell each other their bank account balance. Here we would like to learn the output of max(balance_a, balance_b) and balance_a and balance_b are the private inputs.

In this essay we first present two building blocks:

1. Oblivious Transfer (OT) - This is the most simple construction where one party’s private input is one of two values (a, b), and the other party’s private input is a choice s = (0, 1) that selects either one of the values.

2. Garbled Circuit - This generalizes OT into a circuit of gates and wires where each gate is considered as an oblivious transfer with two inputs.

Then we use these two concepts in to describe Yao’s Protocol, the first two-party computation protocol. From there we can extend it to the multi-party computation called the GMW protocol. We focus on the practical steps and intuitions and briefly discuss the security guarantees, rather than covering the security and formal proofs of the protocols.

Eventually, we discuss one MPC application that is widely used in cryptocurrency custody. Cryptocurrency transaction signatures are computed jointly while each party only holds its own private key share without learning the other parties. In addition to the signature computation, several practical setups are discussed as well - key derivation and key refreshes.

Building Block 1: Oblivious Transfer

A has two values m_0, m_1 and B has a secret choice s that can be 0 or 1. Our goal here is to have A transfer the message where privacy is guaranteed:

1. A does not learn about B’s secret s.
2. B does not learn about m_(1-s) from A (i.e. the message B does not choose).

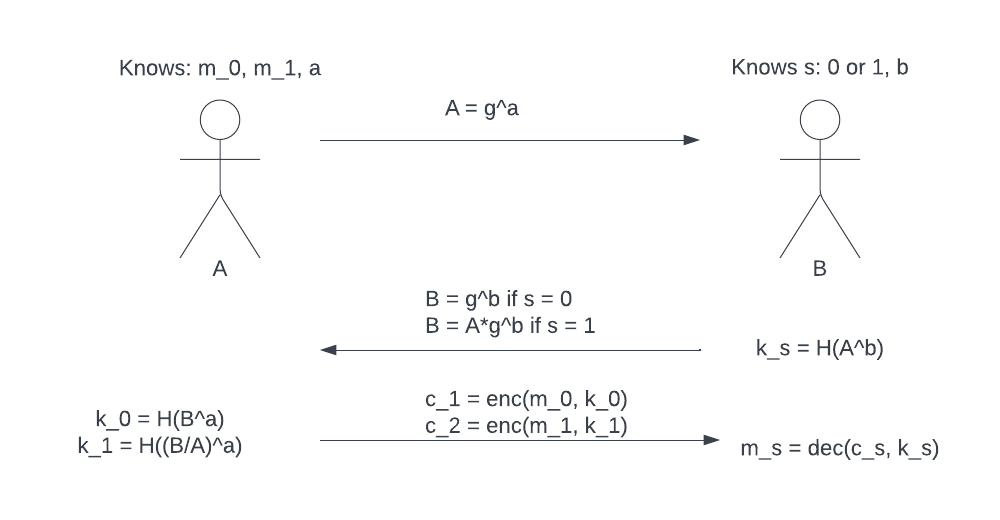
We describe the communications steps following the diagram above:

1. A knows m_0, m_1, a (A’s generated secret value). B knows s, b (B’s secret value).
2. B first does two things: (1) Computes his own key k_s. (2) Sends A a value B based on his choice s. $B = g^b$ if s = 0, $B = A*g^b$ if s = 1. Note that B does not reveal anything of s.
3. Upon receiving value B, A does two things: (1) Computes two different keys k_1 and k_2. (2) Encrypts m_0 and m_1 with k_0 and k_1 respectively and send both ciphertexts to B (c_1 and c_2).
4. B can only decrypt the ciphertext chosen by c that reveals the message of choice: m_s = dec(c_s, k_s).

By the end, we achieve the goals that A does not learn about s and B does not learn about the m that he does not choose. The cost of OT requires 3 rounds of communication and 2 rounds of executions. Let’s trace the correctness of the two possible choice of s by plugging in the respective $k_0, k_1$ vs B value set:

• B chooses s = 0:

$$m_0 = dec(c_0, k_s) = dec(enc(m_0, k_0), k_s) = dec(g^m_0 * B^a, k_s) = dec(g^m_0 * (g^b)^a, k_s) = dec(g^{m_0ab}, A/b) = dec(g^{m_0ab}, g^{a*b}) = m_0$$

• B chooses s = 1:

$$m_1 = dec(c_1, k_s) = dec(enc(m_1, k_1), k_s) = dec(g^m_1 * (B/A)^a, k_s) = dec(g^m_1 * (Ag^b/A)^a, k_s) = dec(g^{m_1ab}, A/b) = dec(g^{m_1ab}, g^{ab}) = m_1$$

Building Block 2: Garbled Circuit

A has the input to the given function, B learns the output of the function only but not the input. In other words, the function takes in an encrypted value of the input and can output the result.

The basic idea here is to encrypt a circuit represented by wires and gates. To do this we assign a pair of keys (k_0, k_1) for every wire, such that for every gate, it is possible to compute the key for the output of the gate.

For example, A and B with a private input a, b try to find out the result of AND(a,b) without learning the private input of each other. (Note that there is some probability for you to “guess” the other person’s input if you pick a = 1 and output = 1, or if a = 1 and output = 0). Let’s define the AND gate with 2 input wires (u, v) and 1 output wire (w). Each input wire are assigned with a pair of key (k_u0, k_u1) and (k_v0, k_v1) and we wish to compute the pair of key for wire w (k_w0, k_w1). We map it to the possible value of an AND gate to a key table - we called it the garbled values:

k_u0	k_v0	k_w0
k_u0	k_v1	k_w0
k_u1	k_v0	k_w0
k_u1	k_v1	k_w1

We then encrypt the keys of the gate in the following format. To take the first row as an example, we have the encrypted value of the output of the gate k_w0 , encrypted with two of the input keys k_u0 and k_v0. This guarantees that given k_u0 and k_v0, only k_w0 can be decrypted. In other words, the receiver of this table can decrypt the value of the output, without learning anything about which input values were used to compute it. This lookup table below is called a garbled gate.

k_u0	k_v0	enc(k_u0, enc(k_v0, k_w0))
k_u0	k_v1	enc(k_u0, enc(k_v1, k_w0))
k_u1	k_v0	enc(k_u1, enc(k_v0, k_w0))
k_u1	k_v1	enc(k_u1, enc(k_v1, k_w1))

Now that we have garbled one gate, we can extend this garbled gate to many composed gates such that the output of one gate is used as an input for the next. Eventually, the final output garbled value can be decrypted to a plain value using a translation table. For example, k_w0 -> 0, k_w1 -> 0. Note that this should only be done at the final output value, not for any of the internal gates!

2PC: Yao’s Protocol

Previously we described a toy example that each party has only 1 input and there is 1 gate. What happens if A and B have multiple inputs? And the gates are composed into multiple gates representing more complex functions? Yao’s protocol applies to a representation of a boolean circuit with multiple gates and multiple inputs.

The protocol is defined as follows:

1. A and B each have n input values: a_1...a_n and b_1...b_n.
2. A sends B the garbled gates for all gates in the circuit (the garbled circuit), along with all the keys corresponding to a_1...a_n. Here we define A’s input wires: $w_{a1}…w_{an}$, B’s input wires: $w_{b1}… w_{bn}$.
3. Now that we have all keys for all A’s inputs, how about the keys for all B’s inputs? Here we perform n oblivious transfers in parallel for b_1...b_n. For each wire i, recall that A has k_i0, k_i1 and B has a choice bit s. At the end of OT, B learns k_is and nothing else.

On efficiency, we have n OT that each has 3 rounds of communication. Each gate has a table of 4 rows where each row requires 2 encryptions. With some optimization, each output requires 2 decryptions.

MPC: The GMW Protocol

This generalizes Yao protocol from 2 to n (>= 2) parties with O(1) communication regardless of the size of the boolean circuit.

Similar to Yao’s protocol, the construction of gates still assigns two keys (garbled values) to each gate. Instead of just a random value, the randomness is a concatenation of the secret shared random values amongst all parties. This differs from the Yao’s protocol in that instead of one party chooses the keys, here we have all parties contributing to the keys.

For each gate, the party computes a 4x1 part of the table in parallel. Given the keys to each input wire, the key for the output wire is revealed. Instead of having one party to evaluate the gates in Yao’s, all parties securely compute the evaluation together in GMW.

MPC Deployment Model for Custody Setup

Now that we have the basic form of a MPC protocol, we discuss one useful MPC application where multiple parties wish to compute a valid signature for a given signature scheme. Each party has one of the keyshares and would not learn any others’ keyshares at the end of computation.

Compute keyshares

The first step is to assign a key share to each party using DKG (distributed key generation). The goal here is to construct the private inputs for each signing party. The protocol is defined as follows:

1. A generates sk_a and B generates sk_b.
2. A sends B an encrypted secret key c = enc(sk_a, n) using the Paillier encryption public key n. A also sends B a proof that that pk_a is generated from sk_a using the homomorphic property.
   • A refresher on Paillier Encryption: Generate private key (p, q) and its public key n = pq. Encryption algorithm work as $enc(m; r) = (1+n)^x * r^n mod n^2$ where r is chosen s.t. gcd(r, n) = 1.
   • This step is useful to make sure the secret key is committed and well-formed.
3. They learn about each other’s public keys pk_a, pk_b and pk = pk_a + pk_b.

Securing Computing a Joint Signature

Now that each party has a secret share, we would like to compute the signature corresponding to a full private key (that either party should not have). The most well known signature schemes we cover here are ECDSA and EdDSA. You may wonder, how does one model a signature scheme in boolean circuits? The random OT model in this paper discusses the encoding of group elements and its field arithmetics in bit strings, which makes it possible to translate a signing scheme into a (large) circuit.

ECDSA:

1. A has sk_a and B has sk_b. Both learns about (R_x, R_y) = sk_a * sk_b * G
2. B generates an encryption of the value k_b^(-1) * ( m' + R_x ⋅ sk_a)

EdDSA:

1. A has r_a and B hash r_b, both learns about R = r_1 * G + r_2 * G.
2. Each computes: e = H(R, Q, m)
3. B sends s_2 = r_2 + sk_2 * e mod q to A.
4. A sends s_1 = r_1 + sk_1 * e mod q and s = s_1 + s_2 to B.

Note: r is chosen randomly instead of a function of the secret key and the message. Although still a valid signature, this makes the MPC produced EdDSA signature deviates from the RFC.

Extension: While here we describe the 2PC version of signing, there are many frameworks and optimizations to accommodate threshold setup with reduced communication cost. This paper describes a widely productionized implementation that involves a preprocessing phase with 3 rounds of communications before the signature is known, and an non-interactive phase to produce a signature share.

Key derivation

Key derivation is an important cryptocurrency primitives that allows one master private key to derive a chain of private keys in a hierarchical way. This is useful to generate multiple deposit addresses (from the corresponding child public keys) while only needing to manage one or few private keys for a custodian. The goal here is to guarantee no single party has the master private key, but we can derive the public key and have each party hold random key shares of the child private keys.

Key Refresh

Another practical aspect of MPC custody is its ability to proactively refresh key shares. This is useful to protect against the scenario that some key shares can be compromised over time.

1. Generate a randomness $r$.
2. Update each private key share by adding or subtracting the same randomness such that the whole key share remains unchanged. $sk_a’ = sk_a - r \mod q$ and $sk_b’ = sk_b + r \mod q$.

Some further extensions are discussed to adapt MPC for a large number of signing parties. White City constructed a set of permissioned facilitator using a trusted setup, allowing a set of permissionless parties of signers. This assumes a semi-authenticated broadcast channel.

References

1. Oblivious Transfer and Garbled Circuits: https://crypto.stanford.edu/cs355/18sp/lec6.pdf

2. Tutorials on Yao’s and BMR: https://cyber.biu.ac.il/event/the-5th-biu-winter-school/

3. MPC custody: https://github.com/unboundsecurity/blockchain-crypto-mpc/blob/master/docs/Unbound_Cryptocurrency_Wallet_Library_White_Paper.md

4. Two party ECDSA: https://eprint.iacr.org/2017/552.pdf